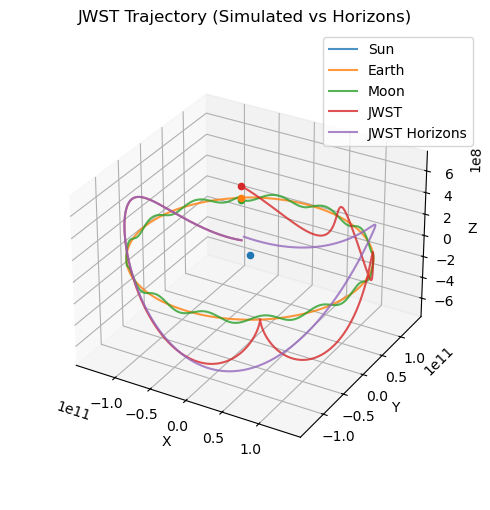
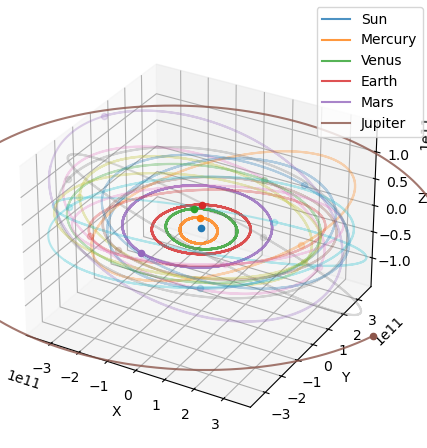
This project involved developing a custom Runge-Kutta numerical solver in Python to model the orbits of all 9 major planets in the Solar System. Using data from NASA's JPL Horizons API, we are able to get data for many near earth asteroids and also JWST. The simulation traces the trajectory of the James Webb Space Telescope as it travels toward the Earth-Sun L2 Lagrange point.
The solver was implemented using both CPU (NumPy) and GPU (CuPy) backends to benchmark performance improvements. An adaptive step-size version of the integrator was also created for greater stability and accuracy. The simulation remains close to real ephemeris data for several months before diverging—demonstrating both the strength and limits of Newtonian integration in an N-body problem.